Cómo se hace la conversión analógica a digital y digital a analógica

Inicio » Hardware » Cómo se hace la conversión analógica a digital y digital a analógica

En nuestro día a día vivimos rodeados de señales analógicas: la voz, la luz, la temperatura, la velocidad de un coche… sin embargo, los ordenadores, móviles y prácticamente cualquier dispositivo electrónico moderno trabajan de forma interna con información digital. Esa diferencia entre cómo funciona el mundo físico y cómo procesan los datos las máquinas obliga a realizar un puente entre ambos mundos: convertir de analógico a digital y, cuando hace falta, volver a convertir de digital a analógico.

Aunque la mayoría de ordenadores actuales son sistemas digitales, todavía existen equipos analógicos especializados, pero son minoría. Cada vez que grabas audio con tu móvil, ves un vídeo en streaming o un sensor mide la temperatura de una habitación, se pone en marcha todo un proceso de conversión A/D y D/A. Entender, aunque sea a nivel conceptual, cómo se hace esta conversión ayuda a comprender mejor límites habituales como el ruido, la calidad de sonido o imagen y el tamaño de los archivos.

Qué es una señal analógica y qué es una señal digital

Para empezar, conviene tener muy clara la diferencia básica: una señal analógica es una señal con valores continuos, mientras que una señal digital se mueve siempre en un conjunto discreto de valores posibles. Es decir, en las señales analógicas las magnitudes pueden adoptar infinitos valores intermedios dentro de un rango, mientras que en las señales digitales solo existen ciertos niveles concretos.

Una señal analógica representa las variables físicas (como tensión, corriente, presión o sonido) mediante una variación continua en el tiempo. Esto significa que si representamos la señal en una gráfica, la curva no da saltos bruscos de un punto a otro, sino que pasa por todos los valores intermedios. De ahí viene lo de “analógica”: es análoga, o similar, a la magnitud real que la genera.

En cambio, una señal digital solo puede tomar valores discretos, normalmente codificados en forma binaria (combinaciones de 0 y 1). No hay infinitos niveles posibles, sino un número finito de peldaños. Cada muestra digital de la señal se corresponde con uno de esos peldaños, que se representan internamente mediante una palabra binaria de cierto número de bits.

Para ilustrarlo con ejemplos cotidianos, una señal que refleja la velocidad de un autobús a lo largo de un viaje sería analógica: el valor pasa progresivamente de 0 km/h hasta, por ejemplo, 50 km/h, y durante ese proceso recorre todas las velocidades intermedias, 1 km/h, 1,1 km/h, 1,2 km/h, etcétera, sin saltarse ninguna. No hay saltos bruscos entre valores.

Por otro lado, el valor de cada muestra de audio en un CD es un buen ejemplo de señal digital. Cada muestra tiene un valor independiente y no existe continuidad entre una y la siguiente. Además, el conjunto de posibles valores para cada muestra es finito, ya que viene determinado por el número de bits con el que se codifica ese audio (por ejemplo, 16 bits por muestra).

Cuando analizamos una señal, sea analógica o digital, nos suele interesar conocer su comportamiento tanto en el dominio del tiempo como en el de la frecuencia. En el dominio del tiempo miramos cómo varía la señal a lo largo de los segundos, mientras que en el dominio de la frecuencia estudiamos qué tonos o frecuencias están presentes y con qué intensidad.

Ancho de banda y espectro de una señal

Para pasar de la visión temporal a la visión frecuencial usamos una herramienta matemática llamada Transformada de Fourier. Esta transformada permite descomponer prácticamente cualquier señal en una suma de ondas sencillas (armónicos) de distintas frecuencias, amplitudes y fases. El conjunto de esas ondas elementales forma lo que se conoce como el espectro de la señal.

El espectro de una señal describe qué componentes frecuenciales la integran: por ejemplo, qué graves, medios y agudos hay en una señal de audio y con qué intensidad contribuye cada uno. No solo es una cuestión académica, sino que tiene un papel clave a la hora de diseñar sistemas de muestreo, filtros o canales de comunicación.

Dentro de ese espectro aparece un concepto fundamental: el ancho de banda. El ancho de banda de una señal se define como la diferencia entre la frecuencia más alta y la más baja que tienen una contribución significativa en el espectro. Por tanto, si llamamos f_min a la frecuencia mínima relevante y f_max a la máxima, el ancho de banda (Bw) será:

Ancho de banda (Bandwidth): Bw = fmax − fmin

Un ejemplo clásico es el del oído humano. Se suele considerar que, en condiciones normales, una persona es capaz de percibir sonidos desde unos 20 Hz hasta unos 20 kHz. Si tomamos esos valores como límites, el ancho de banda del sistema auditivo humano sería aproximadamente:

Bw = fmax − fmin = 20 000 Hz − 20 Hz ≈ 19 980 Hz

Este valor nos da una idea del rango de frecuencias que un sistema debe poder manejar si quiere cubrir completamente la capacidad auditiva humana. Esa cifra será muy importante cuando hablemos de frecuencia de muestreo en la conversión analógica a digital, sobre todo en sistemas de audio.

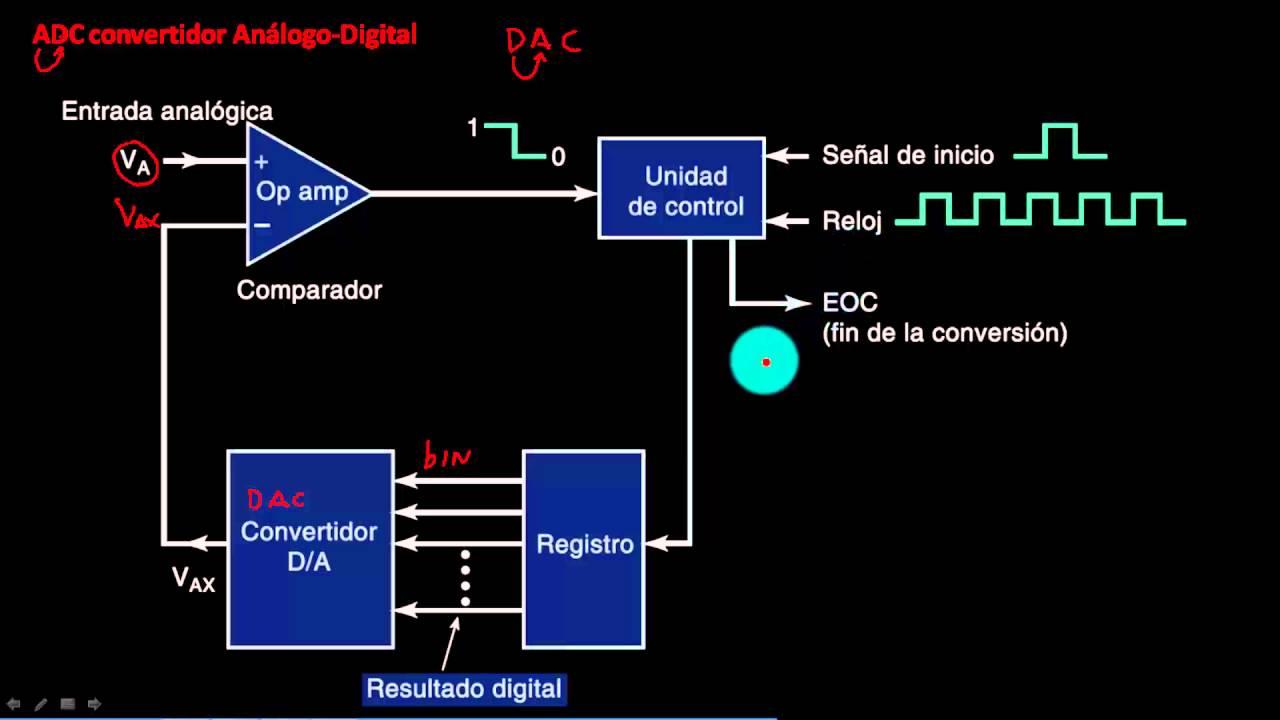
Conversión analógica a digital (A/D)

Cuando queremos que un ordenador procese una señal física (por ejemplo, sonido, temperatura o presión), necesitamos transformarla en una secuencia de números. Ese proceso lo realiza un convertidor analógico-digital (ADC) y se puede dividir, a grandes rasgos, en dos fases: el muestreo de la señal y la cuantificación de las muestras.

La conversión A/D no es un simple “fotografiar” la señal, sino una combinación de cómo de a menudo hacemos esa foto (frecuencia de muestreo) y qué resolución tiene cada foto (cuantificación en bits). De estas dos características dependerá la fidelidad de la copia digital respecto a la señal analógica original, así como el volumen de datos generados.

1. Muestreo de la señal

El proceso de muestreo consiste en tomar valores de la señal analógica a intervalos regulares de tiempo. La distancia temporal entre dos muestras consecutivas se denomina período de muestreo y se representa habitualmente como T_s. A partir de ese período se calcula la frecuencia de muestreo f_s, que no es más que el inverso:

f_s = 1 / T_s

Si el período de muestreo es pequeño, se están tomando muestras muy a menudo y la frecuencia de muestreo será alta. Por el contrario, un período más grande implica que se toman menos muestras por segundo, es decir, una frecuencia de muestreo más baja, lo que se traduce en menos datos para representar la señal.

En la práctica, al elegir la frecuencia de muestreo nos encontramos siempre con un compromiso. Una frecuencia de muestreo alta produce una representación digital que puede seguir con mayor detalle los cambios de la señal original, lo que facilita que podamos reconstruirla después con gran fidelidad. Sin embargo, también genera un flujo de datos mucho mayor, lo que significa más necesidad de almacenamiento, más ancho de banda en transmisiones y mayor carga de procesamiento.

Una frecuencia de muestreo demasiado baja, en cambio, reduce el volumen de información, pero corre el riesgo de que la señal muestreada pierda detalles importantes. Si la frecuencia de muestreo no es suficiente, al reconstruir la señal analógica perdemos información y aparecen distorsiones que no estaban presentes en la señal original, un problema que puede ser muy serio cuando se trata de audio de alta calidad o mediciones críticas.

Para evitar ese problema, entra en juego un resultado teórico muy famoso: el Teorema de Nyquist, también conocido como Teorema de muestreo de Nyquist-Shannon. Este teorema nos indica cuál es la frecuencia de muestreo mínima necesaria para poder recuperar una señal analógica de banda limitada a partir de sus muestras sin pérdida de información.

En forma simplificada, el Teorema de Nyquist dice que, si una señal tiene un ancho de banda B (es decir, su espectro está limitado a frecuencias menores o iguales a B), entonces la frecuencia de muestreo f_s debe ser mayor que el doble de ese ancho de banda. La condición matemática se suele expresar como:

2 · B < f_s

Si esta condición se cumple, en teoría es posible reconstruir la señal original sin introducir errores de muestreo. Si no se cumple, se produce un fenómeno llamado aliasing, en el que componentes de alta frecuencia se “confunden” con componentes de baja frecuencia, deformando por completo la señal reconstruida. Por eso, además de elegir correctamente f_s, se suelen usar filtros paso bajo antes del muestreo para eliminar componentes demasiado altas.

2. Cuantificación de las muestras

Una vez decidida la frecuencia de muestreo y capturados los valores de la señal en cada instante de muestreo, todavía falta un paso: pasar esos valores, que siguen siendo analógicos (continuos), a números discretos que un sistema digital pueda manipular. Ahí entra la fase de cuantificación.

La cuantificación consiste en asignar a cada muestra analógica el valor digital más cercano dentro de un conjunto finito de niveles posibles. Imagina una escalera con un número limitado de peldaños: cada medición de la señal ha de situarse en uno de esos peldaños, nunca entre medias. Cuantos más peldaños haya (más niveles de cuantificación), más preciso será el ajuste de cada muestra al valor real.

Esta operación introduce de forma inevitable un pequeño error, conocido como error de cuantificación. El motivo es que, en la mayoría de los casos, el valor real de la señal no coincide exactamente con ninguno de los niveles disponibles y hay que redondearlo hacia el más cercano. Por eso, a diferencia del muestreo (que puede ser teóricamente perfecto si se cumple el criterio de Nyquist), en la cuantificación siempre aparece cierta imprecisión.

El tamaño de ese error depende, entre otros factores, de la resolución del convertidor A/D. La resolución suele expresarse en bits: con n bits se pueden representar 2ⁿ niveles distintos. A mayor número de bits, más niveles de cuantificación y, por tanto, menor distancia entre niveles. Eso reduce el error de cuantificación máximo y permite representar la señal con más delicadeza.

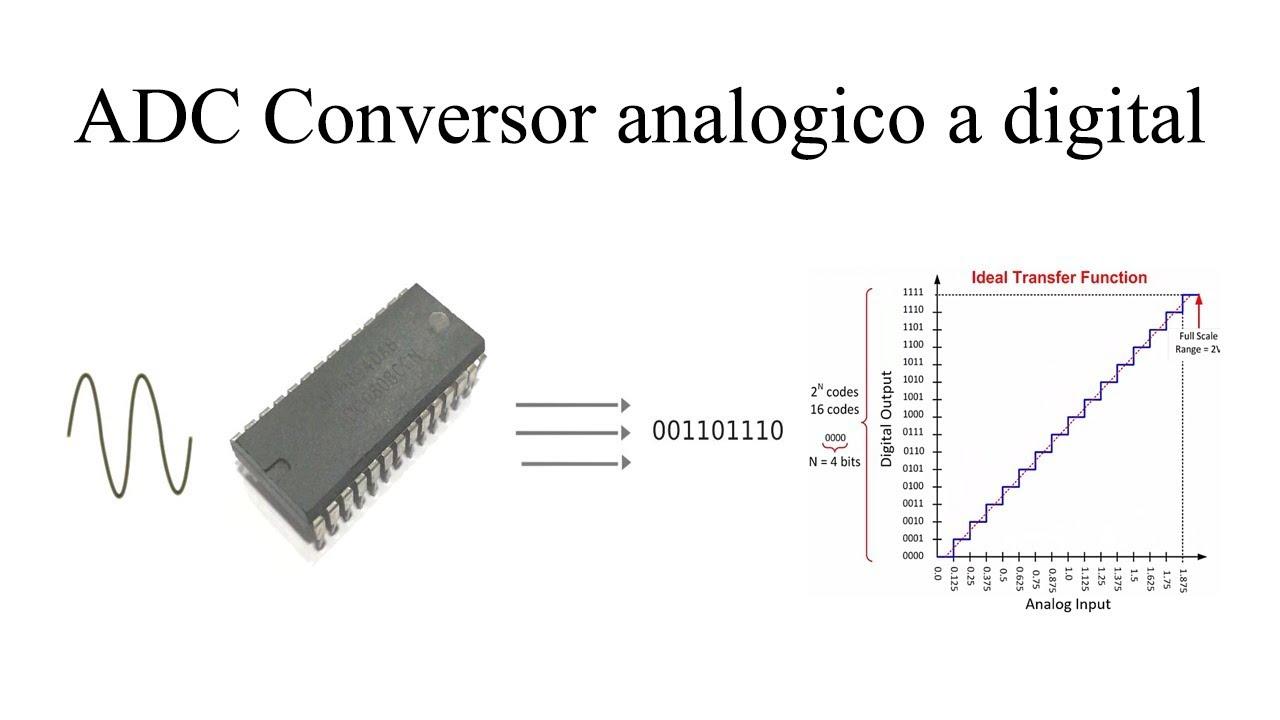
Veamos un ejemplo típico de cuantificación. Imagina que disponemos de un convertidor A/D de 4 bits para digitalizar la lectura de temperatura de un horno industrial. Un conversor de 4 bits puede generar 2⁴ = 16 combinaciones distintas, es decir, 16 valores de salida digitales posibles para cada muestra que se toma de la señal analógica de temperatura.

Supongamos primero que la temperatura del horno se mueve entre 0 ºC y 150 ºC. Podríamos repartir esos 16 niveles de manera uniforme, asignando una palabra de 4 bits a cada incremento de 10 ºC. De este modo, el código binario 0000 representaría 0 ºC, 0001 sería 10 ºC, y así sucesivamente, hasta que 1111 corresponda a 150 ºC. Cada valor real de temperatura que medimos se ajustaría al valor más cercano de entre esos 16 puntos.

Con ese reparto, si la temperatura real fuese, por ejemplo, 23 ºC, el sistema la aproximaría a 20 ºC o 30 ºC según corresponda al valor más próximo. La distancia máxima entre el valor real y el nivel asignado sería de ±5 ºC, que es el error de cuantificación máximo que podemos tener con ese diseño concreto del rango.

Ahora imaginemos que, con el mismo conversor A/D de 4 bits, queremos medir un horno capaz de alcanzar desde 0 ºC hasta 1500 ºC. Seguimos disponiendo de solo 16 niveles, pero ahora el intervalo total es mucho mayor. Si repartimos los niveles de manera uniforme, cada peldaño representará 100 ºC en lugar de 10 ºC. El código 0000 sería 0 ºC, 0001 sería 100 ºC, y así hasta llegar a 1111 como 1500 ºC.

En esta situación, el error de cuantificación máximo sube hasta ±50 ºC, diez veces más que en el caso anterior. Esto muestra claramente cómo a mayor rango con la misma resolución, peor precisión. Para mejorar la precisión sin reducir el rango, necesitaríamos usar un ADC con más bits, lo que incrementaría el número de niveles disponibles.

Conversión digital a analógica (D/A)

Una vez que ya tenemos nuestra señal en forma digital, llega un momento en el que, para interactuar con el mundo real, es necesario volver a convertirla en una señal analógica. Por ejemplo, cuando un reproductor de música envía el sonido a unos altavoces, o cuando una tarjeta gráfica genera la señal analógica para una pantalla que no es completamente digital. Esta tarea recae sobre el convertidor digital-analógico (DAC).

El objetivo de un DAC es transformar una secuencia de códigos digitales (palabras binarias) en una señal analógica suave que se parezca tanto como sea posible a la señal original antes de la conversión A/D. No basta con generar valores sueltos; hay que conseguir una forma de onda continua y filtrada que no tenga saltos bruscos ni escalones excesivamente pronunciados.

Existen distintos tipos de convertidores D/A, cada uno con su propia estructura interna y aplicaciones recomendadas. Dos de los más habituales en la teoría y en la práctica son el mantenedor de orden cero (ZOH) y los DAC multiplicadores (multiplying DAC), muy útiles en sistemas en los que la amplitud de salida depende de una referencia variable.

1. ZOH (Zero Order Hold)

El mantenedor de orden cero, conocido en inglés como Zero Order Hold o ZOH, es probablemente el esquema más sencillo y extendido para reconstruir una señal analógica a partir de sus muestras digitales. La idea es simple: el dispositivo toma cada valor de muestra digital, lo convierte en un valor de tensión o corriente, y lo mantiene constante hasta que llega la siguiente muestra.

De este modo, la salida del ZOH tiene forma de escalera: un tramo horizontal por cada intervalo de muestreo, con saltos en los instantes en los que se actualiza la muestra. Cada peldaño refleja el valor numérico de la muestra en forma analógica. A efectos prácticos, el sistema está asumiendo que la señal se mantiene constante entre muestras, de ahí su nombre de orden cero (no considera variaciones de orden superior).

Sin embargo, esa señal en forma de escalones no es todavía la señal analógica suave que queremos obtener. Para pulir esos bordes y eliminar parte de las componentes de alta frecuencia generadas por los saltos, se hace pasar la salida del ZOH por un filtro paso bajo. El filtro se encarga de suavizar el dentado de la señal, aproximando mucho más la forma de onda original previo al muestreo.

El resultado, si la frecuencia de muestreo se ha elegido correctamente y el filtro está bien diseñado, es una señal por la que no se aprecian los escalones y cuya salida filtrada se aproxima notablemente a la original. En diagramas didácticos, suele representarse una columna de muestras, luego esas mismas muestras mantenidas en forma de escalera y, finalmente, la salida filtrada del paso bajo, que muestra una curva continua sin escalones visibles.

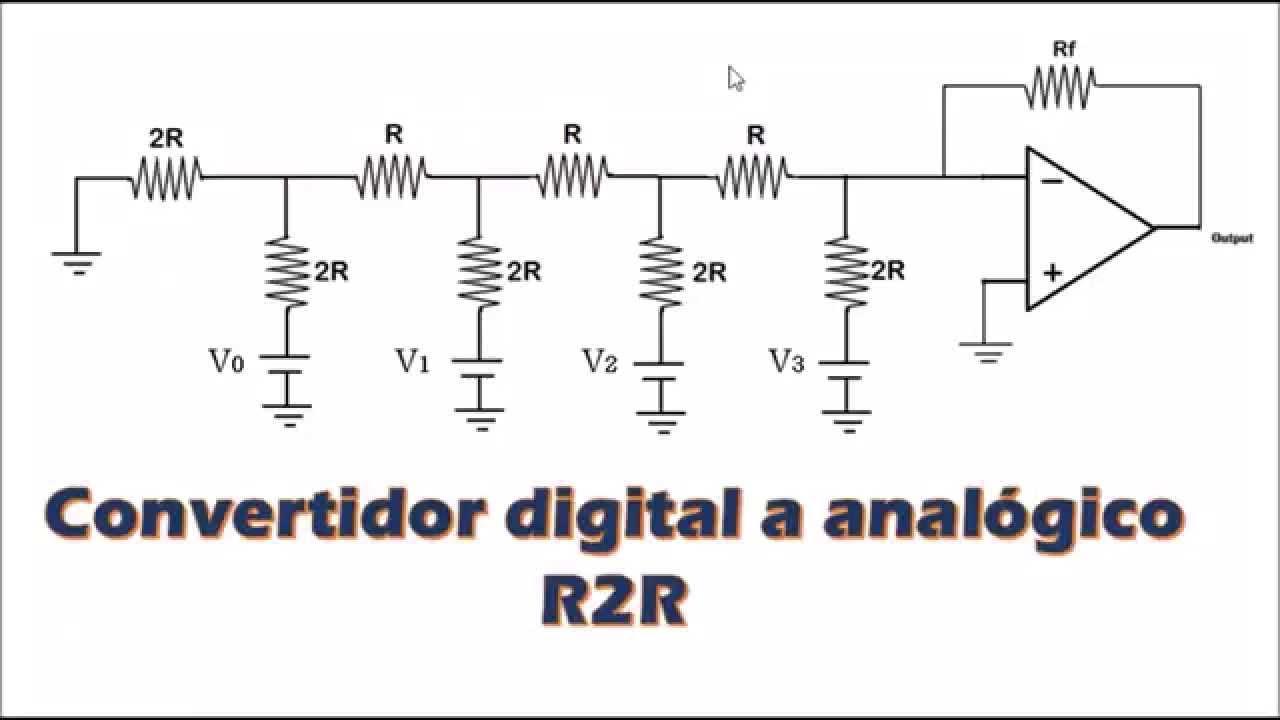
2. Multiplying DAC

Otro tipo interesante de convertidor D/A es el llamado multiplying DAC o DAC multiplicador. Este tipo de dispositivo genera su salida a partir de una corriente o tensión de referencia, modulada por el código digital de entrada. Lo que hace, a grandes rasgos, es aplicar un factor de escala dependiente de la palabra digital sobre la señal de referencia.

Internamente, un DAC multiplicador suele contar con un conjunto de fuentes de corriente o divisores de resistencia que se conectan o desconectan en función de los bits de la entrada digital. Cada combinación de bits activa una serie de corrientes parciales, que se suman para obtener una corriente total proporcional al valor representado por el código binario. De este modo, cada palabra digital selecciona una determinada combinación de corrientes.

La corriente que sale del DAC se puede usar directamente si el circuito posterior trabaja con corriente, o bien se puede convertir en una tensión mediante un amplificador operacional configurado como convertidor corriente-tensión. Esto permite integrar el DAC multiplicador en una gran variedad de aplicaciones, desde generadores de funciones hasta control de ganancia programable o síntesis de señales.

Una de las ventajas de los multiplying DAC es que permiten variar la amplitud de la señal analógica resultante simplemente cambiando la señal de referencia, manteniendo constante el mismo código digital. Así, la salida es, en esencia, el producto entre la referencia y un factor proporcional al valor binario de entrada, lo que hace que este tipo de DAC sea especialmente útil en sistemas de procesado de señales analógicas controladas digitalmente.

En conjunto, tanto los ADC como los DAC constituyen un puente imprescindible entre el mundo analógico y el digital. Su diseño, resolución, velocidad y precisión condicionan de forma directa la calidad de audio, vídeo, medición y control que obtenemos en infinidad de dispositivos. Desde una simple tarjeta de sonido hasta equipos de instrumentación de alta gama, el corazón del intercambio de información con el entorno físico son siempre estos procesos de conversión entre ambos dominios.

Entender a nivel básico qué es una señal analógica y digital, cómo influye el ancho de banda, qué marca el Teorema de Nyquist en el muestreo y por qué la cuantificación introduce un error inevitable ayuda a valorar mejor limitaciones y prestaciones de los sistemas reales, y deja claro que detrás de algo tan cotidiano como reproducir una canción o leer un sensor hay una buena dosis de teoría de señal y electrónica trabajando sin que nos demos cuenta.