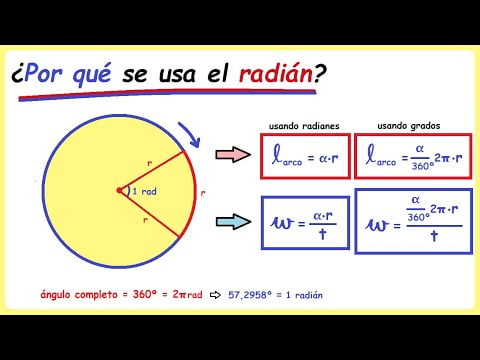
El uso de radianes es una medida angular fundamental en matemáticas y física. A diferencia de los grados, que se utilizan comúnmente en la vida cotidiana, los radianes están basados en la longitud del arco de un círculo y son considerados una medida más natural y consistente para describir el movimiento circular. En esta breve introducción, exploraremos cuándo se debe usar radianes y su importancia en distintas áreas de la ciencia y la tecnología.
La guía definitiva para determinar cuándo utilizar radianes en matemáticas
Los radianes son una unidad de medida angular utilizada en matemáticas y física. Su uso puede ser confuso para algunos estudiantes, pero en realidad es muy simple. La clave es saber cuándo utilizarlos.
En general, se utilizan radianes cuando se trata de problemas que involucran cálculo o trigonometría. Por ejemplo, en el cálculo de integrales o derivadas que involucran funciones trigonométricas como el seno o el coseno, es necesario utilizar radianes.
Además, en la trigonometría, es común utilizar radianes en lugar de grados. Esto se debe a que los radianes tienen una ventaja importante: simplifican las fórmulas trigonométricas. Por ejemplo, la fórmula del seno en radianes es simplemente y=r, mientras que en grados es y=sin(x°).
Otro caso en el que se deben utilizar radianes es en la resolución de problemas relacionados con círculos o arcs. Los radianes son una forma natural de medir ángulos en un círculo, ya que se relacionan directamente con la longitud del arco.
Siempre que estés trabajando con cualquiera de estas áreas, asegúrate de utilizar radianes en lugar de grados.
La elección correcta entre radianes y grados en el uso de calculadoras
¿Cuándo se debe usar radianes?
En matemáticas y física, las medidas angulares se expresan a menudo en radianes o grados. Los radianes son una medida de ángulo que se utiliza en cálculo y trigonometría, mientras que los grados son una medida de ángulo más comúnmente utilizada. Pero ¿cuándo es necesario utilizar radianes en lugar de grados?
La respuesta es simple: cuando se trabaja con funciones trigonométricas como seno, coseno y tangente, es necesario utilizar radianes. Esto se debe a que estas funciones están definidas en términos de radianes y no de grados. Por lo tanto, si se quiere utilizar una calculadora para calcular el seno de un ángulo, por ejemplo, se debe asegurar que el ángulo esté en radianes.
Es importante tener en cuenta que muchas calculadoras científicas y gráficas están preconfiguradas para trabajar con radianes. Por lo tanto, es posible que deba cambiar la configuración de su calculadora para trabajar con grados. Si se está trabajando con una función trigonométrica y la respuesta no parece estar en el rango esperado, es posible que se deba a que la calculadora está configurada para trabajar en grados en lugar de radianes.
Asegúrese de que su calculadora esté configurada correctamente para trabajar con radianes y no se confunda si la respuesta parece estar incorrecta.
Radián: la medida angular esencial en matemáticas y física
Radián: la medida angular esencial en matemáticas y física
En matemáticas y física, se utilizan diferentes unidades de medida para expresar ángulos. Entre ellas, el radián es considerado la medida angular esencial. El radián se define como la medida del ángulo central que abarca un arco de circunferencia cuya longitud es igual al radio de dicha circunferencia.
El uso de radianes es preferido en muchas situaciones debido a su simplicidad y conveniencia matemática. En comparación con otras unidades de medida, el radián elimina constantes de conversión y simplifica algunas fórmulas matemáticas. Además, el radián es la única medida angular que no requiere el uso de constantes específicas para su conversión a otras unidades de medida.
El uso de radianes es especialmente importante en el cálculo y en la física teórica, donde se utilizan funciones trigonométricas y cálculos de derivadas e integrales. En estos campos, el uso de radianes puede simplificar drásticamente los cálculos y reducir el riesgo de errores.
Su uso simplifica los cálculos y elimina la necesidad de constantes de conversión. El radián es especialmente importante en el cálculo y la física teórica, donde puede reducir el riesgo de errores y simplificar los cálculos.
