En matemáticas, una partición es una forma de dividir o separar un conjunto en subconjuntos más pequeños y específicos. Las particiones son comúnmente utilizadas en diversas ramas de las matemáticas, como la teoría de conjuntos, la teoría de números y la teoría de grafos. Las particiones pueden ser útiles para resolver problemas complejos al reducir el tamaño y la complejidad del conjunto original y permitir una mayor comprensión y análisis de las propiedades y relaciones de sus subconjuntos. En este artículo, exploraremos en detalle qué son las particiones en matemáticas y cómo se pueden aplicar en diferentes áreas de estudio.
¿Cuando un conjunto es partición de otro?
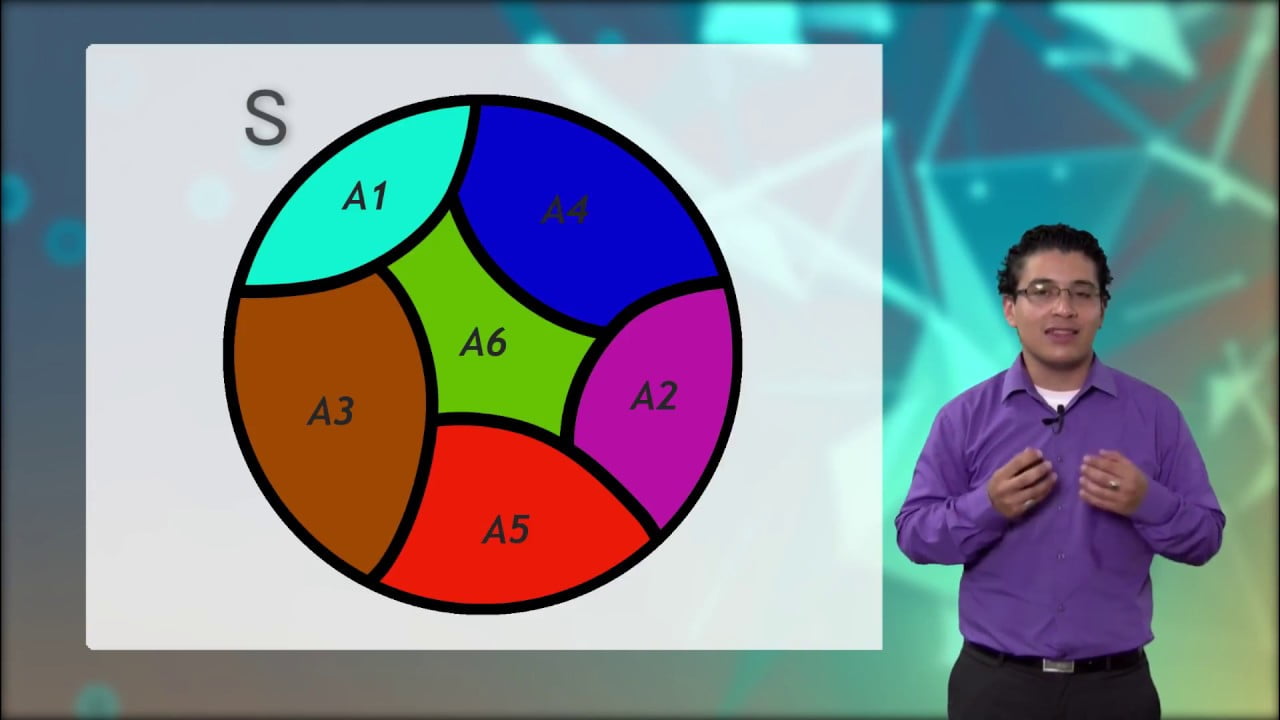
En matemáticas, una partición de un conjunto es una colección de subconjuntos no vacíos del conjunto original, donde cada elemento del conjunto original está contenido en exactamente uno de los subconjuntos de la partición.
Es decir, si tenemos un conjunto A y una partición P de A, entonces:
- Cada elemento de A debe estar en al menos uno de los subconjuntos de P.
- Cada subconjunto de P debe ser no vacío.
- Los subconjuntos de P deben ser disjuntos entre sí.
En otras palabras, no puede haber elementos que pertenezcan a más de un subconjunto de la partición.
Un ejemplo sencillo de partición es la siguiente:
Sea A = {1, 2, 3, 4, 5, 6}.
Entonces, una posible partición de A sería:
- {1, 4}
- {2, 5}
- {3, 6}
En este caso, cada elemento de A está en exactamente uno de los subconjuntos de la partición, cada subconjunto es no vacío y los subconjuntos son disjuntos entre sí.
¿Qué es la participación de un conjunto?
La participación de un conjunto se refiere a la división de un conjunto en subconjuntos disjuntos de tal manera que cada elemento del conjunto original sea asignado a exactamente uno de los subconjuntos creados. Esta división se conoce como una partición del conjunto.
En matemáticas, las particiones son una herramienta importante para resolver problemas de combinatoria, estadística y teoría de conjuntos. Se utilizan para contar el número de formas en que se pueden dividir objetos en grupos, para analizar relaciones de equivalencia entre elementos de un conjunto y para expresar soluciones a problemas en términos de particiones.
Por ejemplo, si se tiene un conjunto de seis elementos y se desea dividirlo en dos subconjuntos de manera que cada subconjunto tenga exactamente tres elementos, se puede realizar una partición del conjunto. Una posible partición podría ser {1, 2, 3} y {4, 5, 6}. Otra partición podría ser {1, 4, 5} y {2, 3, 6}. En ambos casos, cada elemento del conjunto original se asigna a exactamente uno de los subconjuntos.
¿Quién creó las particiones?
Las particiones en matemáticas son un conjunto de números enteros que sumados dan un número determinado. Este concepto fue introducido por el matemático indio Srinivasa Ramanujan en la década de 1910.
Ramanujan es considerado uno de los matemáticos más importantes del siglo XX y su trabajo en teoría de números ha sido fundamental para el desarrollo de esta rama de las matemáticas. Entre sus logros se encuentra la creación de una fórmula para el número pi que permitió calcularlo con una precisión nunca antes vista.
En cuanto a las particiones, Ramanujan fue capaz de desarrollar una fórmula para calcular el número de particiones de un número determinado. Esta fórmula ha sido estudiada y mejorada por muchos otros matemáticos a lo largo de los años y sigue siendo un tema de investigación en la actualidad.
